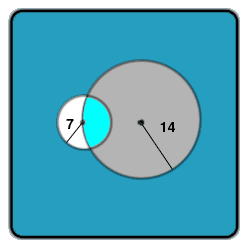
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.
(P.S -The answer might not be elegant)
If we assign the center with the circle with 14cm as the origin (0,0), and the 7cm circle to be centered along the x-axis (-14,0), we can then compute where the chord, defined where the two circles intersect, intersects the x-axis.
14cm circle equation: x
2 + y
2 = [14]
2 7cm circle equation: (x - [-14])
2 + y
2 = [7]
2 The equations can be re-written as:
y
2 = 196 - x
2 y
2 = 49 - (x + 14])
2 Combining the two equations, we then solve for x:
[196 - x
2 = 49 - (x + 14])
2x = -49/4
The length of the sagitta of the chord to the 14cm circle's circumference is:
14 - |-49/4| => 7/4
and the length of the sagitta of the chord to the 7cm circle's circumference is:
7 - |7/4| => 21/4
The area of a circle segment is given by the equation
R
2*cos
-1([R - h]/R) - (R - h)*SQRT(2*R*h - h
2)
where R is the circle's radius and h is the length of the sagitta.
The area of the arc segment of the 14cm circle is then:
14
2*cos
-1([14 - 7/4]/14) - (14 - 7/4)*SQRT(2*14*7/4 - 7/4
2)
= 196*cos
-1(7/8) - 343/16*SQRT(15)
~= 16.02357953 cm
2And the area of the arc segment of the 7cm circle is then:
7
2*cos
-1([7 - 21/4]/7) - (7 - 21/4)*SQRT(2*7*21/4 - 21/4
2)
= 49*cos
-1(1/4) - 49/16*SQRT(15)
~= 52.72667601 cm
2The combined area -- the common area of both circles -- is then approximately:
16.02357953 cm
2 + 52.72667601 cm
2 =>
68.75025554 cm2 Edited on February 10, 2008, 9:16 am
|
|
Posted by Dej Mar
on 2008-02-10 07:24:23 |



