Tic-Tac-Toyola is a variation of Tic-Tac-Toe with money. Instead of naughts and crosses (0s and Xs for Americans) being placed at the whim of alternating players, players vie for placement control at each turn by bidding some amount in a currency from an account under their control. The high bid decides the placement, with that bid amount being deducted from the corresponding player's account. Bids are in continuous units, so we can neglect the possibility of tie bids as unlikely.

There are two players: C(rosser) and N(aughty). X is placed first, and player C is declared winner if 3 Xs appear in a row before 3 Os appear in a row. If neither player achieves three in a row, N is declared winner. Thus, a game of Tic-Tac-Toyola will always have a winner.

C and N have been playing for some time and have reached the position:

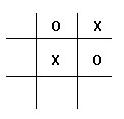
(1) Assuming players are following optimal strategies, show that the outcome is independent of whether bidding is conducted secretly (by sealed bids) or openly (with players offered at each turn the possibility to outbid their opponent).

(2) Show that a player who is following an optimal strategy would not change his bid if he were to learn his opponent's account balance.

(3) Show that N can force a win if and only if he has in excess of twice as much money as C.

Note: Anyone interested in learning more about the Tic-Tac-Toyola family of games is invited to visit http://www.diplom.org/Zine/S2007R/Mayer/tictactoyola.htm

For those that do not understand the term, a cat's game is a tie game in a standard tic-tac-toe game, i.e., where there are neither three X's nor three O's in a row in a filled tic-tac-toe grid. I shall use this term here to apply to the same filled grid condition sans "tie game".

Crosser needs only win one of the next two control placements to insure a win. Failing that, Crosser needs to win the following two to prevent Naughty from winning by a cat's game. The final placement control being predetermined as a set placement of an X and unimportant by either as to who then controls the placement.

Working backwards, to prevent Naughty from winning by a cat's game, Crosser needs c = 2*(n+1), such that n is the current balance at that point of Naughty's account amount. Naughty, then needs -- proving point (3) -- 2*(c + 1) to prevent Crosser from having either of the first two control placements.

------
Crosser's win by first control placement:

 |O|X
-+-+-
 |X|O
-+-+-
X| |

If the first control placement is won by Naughty, Naughty would need to place the X in one of the empty sides. As the grid is diagonally symmetrical top-right to bottom-left, it matters not which of the two sides. If Naughty places the X in one of the empty corners (other than the automatic win for Crosser, of course), he leaves either of the other two corners open for crosser to win, such that Crosser would only need win one of the next two placement controls.

 |O|X
-+-+-
X|X|O
-+-+-
 | |

If the second control placement is won by Crosser, his placement of the O in the remaining empty side will give X, hence Crosser, a win of three X's on one of the two diagonals.

X|O|X  O|O|X  X|O|X
-+-+-  -+-+-  -+-+-
X|X|O  X|X|O  X|X|O
-+-+-  -+-+-  -+-+-
O|O|X  X|O|X  X|O|O

Edited on April 27, 2008, 9:29 pm

Posted by Dej Mar on 2008-04-27 14:46:54