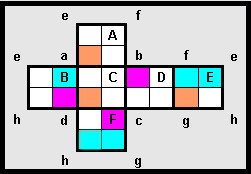
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
(In reply to
Clarifications?? by ed bottemiller)
I read it to mean that within each square face, the four digits of its four-digit square are read either clockwise or counterclockwise, starting at a subsquare that is colored either magenta or orange, and that choice of clockwise or counterclockwise is made so that the rest of the puzzle can be solved.
Likewise, the three-digit square for a given vertex starts at an adjacent subsquare colored either magenta or cyan. Of necessity, it goes either clockwise or counterclockwise as there are only two possible orders for the remaining two digits.
|
|
Posted by Charlie
on 2008-04-30 15:37:46 |




