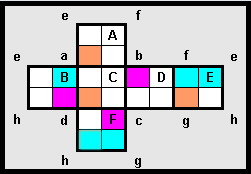
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
(In reply to
re: Clarifications?? by Charlie)
Thanks, Charlie! This seems a reasonable interpretation, e.g. that "rotation" could be either clockwise or counterclockwise from the midpoint of a side of the cube, and that "defined by need" really means "try both directions -- but ostensibly only one will lead to an overall solution". I find 19 3-digit squares, and 45 4-digit squares (excluding any with a digit zero). These will probably have to be at least doubled to account for rotating in either direction. The starting point, I assume, will be to decide how many of the "commencement cells" can be identified from the three color clues. Though he doesn't say so, I assume that a final solution may assume these three color premisses (even though he says he was unsuccessful when he was using them: I guess he means that a "close" solution was available, but that two of the vertex sets were duplicates.) It is not clear whether a 4-digit square and its digital reverse would each count as a "unique" solution; I am not sure whether his penultimate Note is intended to address that matter (or any other -- it's too vague). I hope he has ascertained and verified that there is indeed a solution meeting (some) "uniqueness" criterion.




