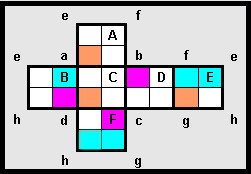
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
Charlie, it seems we have this one to ourselves still. I tried drawing inferences from the colored squares, and found this helpful. I numbered the squares by rows, viz 1-2, 3-4, 5-12, 13-20, 21-24. The six sides are already denoted by capital letters A..F, and the eight vertices by small letters a..h. (There are 44 4-digit squares, not 45 as I posted before; each can be read clockwise or counterclockwise.)
For the 4-digit sides this gives as the commencement squares: 03 for side A, 14 for side B, 15 for side C, 09 for side D, and 19 for side E. However, for side F (21-22-23-24) there seems to be too many clues: 21 is plain, 22 is magenta (so must be first digit of 4-digit side F as well as first digit of vertex c), but since 23 is orange, that also is indicated as the first digit of 4-digit side F (and not of vertex h). This can be resolved, since there are three squares (1296, 2916, 9216) which use the same four digits, and the pair 1296 and 9216 can occur together. There seem to be two other pairs of squares sharing four digits (1369,1936; and 1764,4761), if that is useful.
For the 3-digit vertices, this gives 06 for vertex a, 09 for vertex b, 22 for vertex c, 14 for vertex d, 12 for vertex e, 11 for vertex f, 24 for vertex g, but none of the squares at vertex h (i.e. 13, 20, 23) is colored. Shall we assume that the three color clues are not exhaustive, i.e. that a square may begin a vertex square triad without being colored? More, anon...




