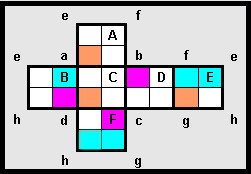
I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.
To emulate my "feat":
- a [Magenta]
Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange]
Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan]
Cyan cell signifies the first cell only of a 3 digit square.
The digits must be applied to each face by rotation, the direction is defined by need.
"A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled.
 Note:
Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.
But then, there is still the challenge for 6 unique faces and 8 unique vertices.
(In reply to
re: Biggest problem I see! by brianjn)
This is the issue I raised in my Comment 5. For side F, I found that TWO 4-digit squares could be found, one starting in the upper right (magenta, label F) and the other in the lower left (originally orange), so I assumed this was intentional. I also noted that that diagram left no designated square for the h vertex, though the original problem did not state that a starting square could be directly inferred for each square (and I was puzzled since brianjn's replies seemed to state that a start could be inferred for all the squares).
From the latest comment, I read it to say that the lower left square of side F should be colored cyan, and presumably everything else kept as is (e.g. the lower right of F is still cyan). My screen is still coming up with the original colors.
I trust that all other clues and the diagram have been double checked to be sure that there are no other errors, AND for brianjn to affirm that (1) he has a proven solution to his challenge, i.e. that all six sides have unique squares and that all eight vertices have unique squares, and (2) that there is only one such solution. Unfortunately the text says only that the proposer has found a "nearly complete" solution (with the square at two of the vertices being the same), and that is presumably the "my feat" which is reproduced by the color clues. Why should we look for such, if the proposer did not in fact know that such exists?
Also, I am still not clear the answer to my question about including the "rotational direction" along with the actual square when deciding "uniqueness" -- if the same square is read clockwise in one usage, and counterclockwise in a second, is that allowed or not?? Also, does this apply to both the 3-digit and 4-digit squares? Perhaps the proposer knows what applies to the solution he has in mind, but it makes a difference how we code the task in trying to find solution(s).




