I applied one of the digits 1 through 9 to each cell of the provided net of a cube.
My object was to create a unique 4 digit square number on each face. At the same time I required each vertex to be a 3 digit square. I failed in that objective!
I have 6 unique 4 digit squares but I have duplicated just one of my vertices.

To emulate my "feat":
- a [Magenta] Magenta cell is both the first digit of a 3 and 4 digit square
- an [Orange] Orange cell signifies the first digit of only a 4 digit square, while
- a [Cyan] Cyan cell signifies the first cell only of a 3 digit square.

The digits must be applied to each face by rotation, the direction is defined by need. "A" through "F" represent the 6 faces of the cube while "a" through "h" represent the vertices of the cube when fully assembled. Note: Within the range allowed several squares utilise the same digits, and this is allowed by virtue of the commencement cell.

---

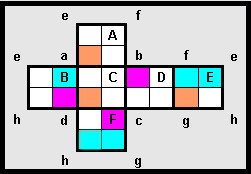
But then, there is still the challenge for 6 unique faces and 8 unique vertices.

(In reply to Charlie and ed bottemiller by brianjn)

ed bottemiller,
something I did not address which Charlie has taken up was the "challenge".

On Perplexus some pose a trailing "bonus" question.  Why?
Some problems don't allow one to further create the next problem, but some allow further provocation of thought.

Provocation of thought?  Yes, you are offered a challenge to explore more, or in this case I posed a question but offered an ultimate.


Is that fair?

Posted by brianjn on 2008-05-03 11:12:41