Place the numbers 1 to 9 once in each row, column,
long diagonal (marked with a heavy dot) and every 3x3 grid.
The '
cage' inclusions (individually coloured regions) indicate the sum or the product of the numbers in those cells.
Unlike Killer Sudoku, the same number may appear more than once in a cage. So, 36x in a cage which overlaps the 3x3 grids may contain two 6s and a 1.
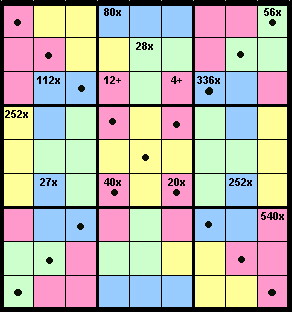 My inspiration for this puzzle came from a variety of puzzles posted by Pete and Will at http://sudexel.com/forum/index.php
My inspiration for this puzzle came from a variety of puzzles posted by Pete and Will at http://sudexel.com/forum/index.php
My thanks goes to brianjn for his hard work in producing the graphic.
(In reply to
re(3): Solution by brianjn)
I created a spreadsheet of the "xy" 9 x 18 suggested previously.
With 2 cells making up one, each cell presented with a numeral and operator was supplied with a formula that drew on "lower half cells" of each referenced cage.
For comparison I copied the image that is in the body text and pasted it into my spreadsheet.
Outside the 9 x 18 grid I wrote formulae to sum each column, every second horizontal row of "half cells" and each diagonal. [The sum in each case is 45].
With the image as a comparison, and the summations suggested, one would have a valid solution.
Having played for awhile I entered Penny's solution.
Yes, Dej Mar, I expect that from your description your approach was closely related; a worthy tool to assist a solution to problems such as this.
Edited on May 30, 2008, 4:56 am
|
|
Posted by brianjn
on 2008-05-30 03:28:50 |




