When overlapped the 5 Olympic rings enclose 9 regions.
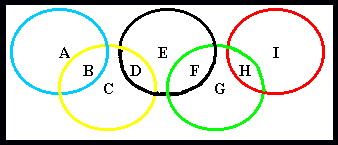
Place each of the numbers from 1 to 9 in a separate region so that:
A + B = B + C + D = D + E + F = F + G + H = H + I = M
where M represents the total of each ring.
How many values for M can you find?
How many arrangements for each M can you also find (discount total reversal of order)?
There are three values for M: 11, 13 and 14.
There is only one arrangement (plus one for reversal of order) for each value 11 and 14 of M. For 13, there are two arrangements (plus one reversal of order for each arrangement):
11 --> 8,3,7,1,6,4,5,2,9 & reversal: (9,2,5,4,6,1,7,3,8)
13 --> 4,9,1,3,8,2,5,6,7 & reversal: (7,6,5,2,8,3,1,9,4)
13 --> 7,6,5,2,3,8,1,4,9 & reversal: (9,4,1,8,3,2,5,6,7)
14 --> 5,9,2,3,4,7,1,6,8 & reversal: (8,6,1,7,4,3,2,9,5)
A+B = B+C+D = D+E+F = F+G+H = H+I = M
8+3 = 3+7+1 = 1+6+4 = 4+5+2 = 2+9 = 11
9+2 = 2+5+4 = 4+6+1 = 1+7+3 = 3+8 = 11
4+9 = 9+1+3 = 3+8+2 = 2+5+6 = 6+7 = 13
7+6 = 6+5+2 = 2+8+3 = 3+1+9 = 9+4 = 13
7+6 = 6+5+2 = 2+3+8 = 8+1+4 = 4+9 = 13
9+4 = 4+1+8 = 8+3+2 = 2+5+6 = 6+7 = 13
5+9 = 9+2+3 = 3+4+7 = 7+1+6 = 6+8 = 14
8+6 = 6+1+7 = 7+4+3 = 3+2+9 = 9+5 = 14
Edited on June 4, 2008, 11:58 pm
|
|
Posted by Dej Mar
on 2008-06-04 11:56:20 |




