When overlapped the 5 Olympic rings enclose 9 regions.



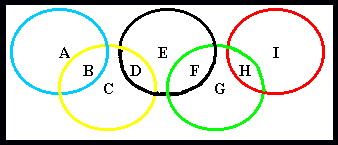
Place each of the numbers from 1 to 9 in a separate region so that:

A + B = B + C + D = D + E + F = F + G + H = H + I = M

where M represents the total of each ring.

How many values for M can you find?
How many arrangements for each M can you also find (discount total reversal of order)?

(In reply to re: Solution by brianjn)

Using the Trachtenberg system of rapid mental calculation, I came up with the following four answers:

M = 11 (8 3 7 1 6 4 5 2 9)
M = 13 (4 9 1 3 8 2 5 6 7)
M = 13 (7 6 5 2 3 8 1 4 9)
M = 14 (5 9 2 3 4 7 1 6 8)

Posted by Penny on 2008-06-05 01:31:26