The understood Venn diagram is of 3 circles overlapping each other to form 7 enclosed regions.

Consider this structure being imposed upon the "Olympic Rings" to create 15 regions.



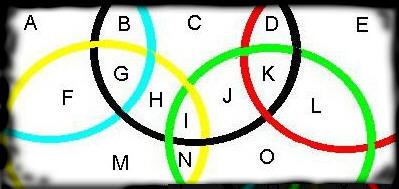
Place one number from 1 to 15 in each region so that the middle top ring (Black) has a total of Z + 2 while the other 4 total Z each.

Ring Values:

1.  A  B  F  G              [Z]
2.  B  C  D  G  H  I  J  K  [Z+2] (Black)
3.  D  E  K  L              [Z]
4.  F  G  H  I  M  N        [Z]
5.  I  J  K  L  N  O        [Z]

Note: Olympic Rings has fewer overlaps.

(In reply to Solution by Penny)

Re: "I found nine distinct values for Z, with literally thousands of arrangements that produce them."

15,148 total arrangements found, not excluding redundant ones (mirror images, etc.)

So this can't be right.

 

 

 

 

Edited on June 9, 2008, 9:15 am

Posted by Penny on 2008-06-09 09:12:39