The understood Venn diagram is of 3 circles overlapping each other to form 7 enclosed regions.

Consider this structure being imposed upon the "Olympic Rings" to create 15 regions.



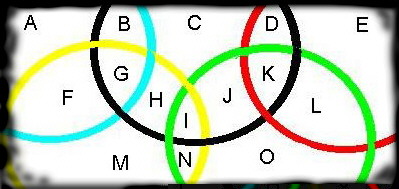
Place one number from 1 to 15 in each region so that the middle top ring (Black) has a total of Z + 2 while the other 4 total Z each.

Ring Values:

1.  A  B  F  G              [Z]
2.  B  C  D  G  H  I  J  K  [Z+2] (Black)
3.  D  E  K  L              [Z]
4.  F  G  H  I  M  N        [Z]
5.  I  J  K  L  N  O        [Z]

Note: Olympic Rings has fewer overlaps.

(In reply to re: Solution by Penny)

Why can't that be right?

The number is divisible by 2, as each solution has a reverse.

There's no need for the number to be divisible by 9 as there may be a different number of solutions for different totals.

Was there another criterion for saying the number is impossible?

Posted by Charlie on 2008-06-09 12:20:00