The understood Venn diagram is of 3 circles overlapping each other to form 7 enclosed regions.

Consider this structure being imposed upon the "Olympic Rings" to create 15 regions.



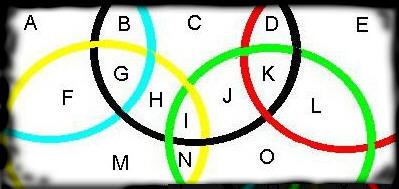
Place one number from 1 to 15 in each region so that the middle top ring (Black) has a total of Z + 2 while the other 4 total Z each.

Ring Values:

1.  A  B  F  G              [Z]
2.  B  C  D  G  H  I  J  K  [Z+2] (Black)
3.  D  E  K  L              [Z]
4.  F  G  H  I  M  N        [Z]
5.  I  J  K  L  N  O        [Z]

Note: Olympic Rings has fewer overlaps.

(In reply to re(2): Solution by Charlie)

There was no other criterion. It just seemed like an unusually large number of possible solutions (for Perplexus.) But maybe not. The puzzle never stated that the solution had to be unique in some sense. 

Of course the number is cut exactly in half by requiring A < E.

(I held off for a day on this one, to give the analytical solvers a chance with it, before applying my brute force program.)

 

 

Edited on June 9, 2008, 12:44 pm

Posted by Penny on 2008-06-09 12:34:57