The understood Venn diagram is of 3 circles overlapping each other to form 7 enclosed regions.

Consider this structure being imposed upon the "Olympic Rings" to create 15 regions.



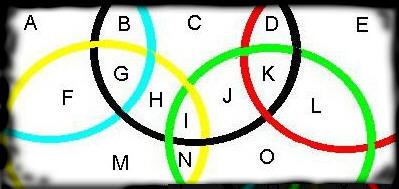
Place one number from 1 to 15 in each region so that the middle top ring (Black) has a total of Z + 2 while the other 4 total Z each.

Ring Values:

1.  A  B  F  G              [Z]
2.  B  C  D  G  H  I  J  K  [Z+2] (Black)
3.  D  E  K  L              [Z]
4.  F  G  H  I  M  N        [Z]
5.  I  J  K  L  N  O        [Z]

Note: Olympic Rings has fewer overlaps.

(In reply to re: Solution by Penny)

I noted your first two comments shortly after you had posted and was amazed seeing as how I had developed this in a spreadsheet and could only come up with Z equal to 42 and so was feeling that was a unique solution but I wasn't about to make that claim in the problem.

I tried to enter some of your values in the sheet and they were in deviance with your claim.  This morning I found that reason.  I had duplicated part of my spreadsheet and while playing with values had cross-referenced two data values!!

Posted by brianjn on 2008-06-09 22:00:55