Trisecting an angle, using only compass and straight edge, was one of the great classical problems of antiquity.

Modern mathematics has proved it impossible, but here is a simple and ingenious mathematical cardboard device that trisects accurately:


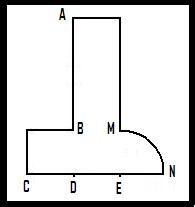
If you place it properly, so the edge AB passes through the vertex of the given angle, one side of the angle passes through point C, and the other side tangents the arc MN (arc of the circumference centered at E and radius ED), the lines traced from the vertex through the points D and E trisect exactly the angle.

Prove it.

The device is perfectly drawn to scale, so you can get any information you need about lengths, parallelism, intersections etc...

(In reply to ------------------ by pcbouhid)

I somewhat share your lament.

I recall seeing this many years ago, in fact I believe it is in one of my paperbacks (that I haven't looked at for ages).

With our respective CAD programs we can sometimes be somewhat dismissive of what came before. 

As a poor analogy, while reading and the electricity supply fails do you have a backup, a candle, a paraffin lamp? 

There is something to be said for "first principles"; at least we know that there is something solid from which we can work.  While it might be argued that this is not "first principles" it could well be a handy device in the toolkit of a "pencil and paper" draftsman or one needing such tools.

Posted by brianjn on 2008-09-01 06:11:05