I was walking along the road one day when I spied a cord of some sort lying in my path. From my vantage point, as I was approaching the cord, I could not tell if it was knotted or not.
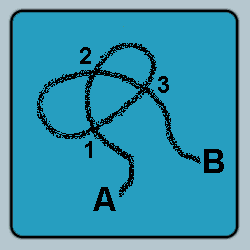
What is the probability that the cord was knotted?
Assuming the cord is continous from end-point A to end-point B, and not fused at any of the three intersection, 1, 2 or 3, there is a 2/8, i.e. 25% chance the cord will knot when the two end-points, A and B, are drawn away from each other.
A-1-2-3-B O = over U = under
O O O
O O U
O U O Knot
O U U
U O O
U O U Knot
U U O
U U U
Of the eight permutations, only two exist where the adjacent intersecting points of the cord alternate between passing over or under the looped cord, thus there are only two permutations where the cord will knot.
|
|
Posted by Dej Mar
on 2008-10-04 09:46:01 |



