A figurate number stack is built using only the digits 0 through 9 exactly once.
Each tier is a
figurate number of the order labelled; no number has a leading zero.
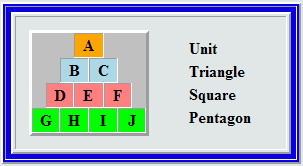
How many solutions can you offer?
The program below originally produced the following table in 2-digit triangle order, but I re-sorted it to be in order of the "unit" number.
I'm not sure what counts as a valid unit number, but what is shown is what is left after the triangular, square and pentagonal numbers use up all but one of the ten digits.
1 78 324 9560
2 45 361 9087
2 91 784 6305
3 15 784 6902
3 21 784 9560
4 10 529 3876
4 28 169 5370
4 28 196 5370
4 28 961 5370
4 36 289 5017
4 78 169 2035
4 78 196 2035
4 78 961 2035
4 91 576 2380
6 15 324 9087
6 15 784 3290
6 91 784 2035
7 36 289 4510
7 45 169 2380
7 45 196 2380
7 45 961 2380
8 36 729 4510
9 21 784 6305
9 36 784 1520
9 36 784 2501
9 78 324 6501
DIM t$(81), s$(81), p$(81)
CLS
FOR n = 1 TO 81
tri = n * (n + 1) / 2
tr$ = LTRIM$(STR$(tri))
sq = n * n
sq$ = LTRIM$(STR$(sq))
pent = n * (3 * n - 1) / 2
pe$ = LTRIM$(STR$(pent))
IF LEN(tr$) = 1 THEN COLOR 12: PRINT tr$; " "; : COLOR 7
IF LEN(sq$) = 1 THEN COLOR 14: PRINT sq$; " "; : COLOR 7
IF LEN(pe$) = 1 THEN COLOR 10: PRINT pe$; " "; : COLOR 7
IF LEN(tr$) = 2 THEN
good = 1
FOR i = 1 TO LEN(tr$) - 1
IF INSTR(i + 1, tr$, MID$(tr$, i, 1)) THEN good = 0: EXIT FOR
NEXT
IF good THEN
tCt = tCt + 1
t$(tCt) = tr$
END IF
END IF
IF LEN(sq$) = 3 THEN
good = 1
FOR i = 1 TO LEN(sq$) - 1
IF INSTR(i + 1, sq$, MID$(sq$, i, 1)) THEN good = 0: EXIT FOR
NEXT
IF good THEN
sCt = sCt + 1
s$(sCt) = sq$
END IF
END IF
IF LEN(pe$) = 4 THEN
good = 1
FOR i = 1 TO LEN(pe$) - 1
IF INSTR(i + 1, pe$, MID$(pe$, i, 1)) THEN good = 0: EXIT FOR
NEXT
IF good THEN
pCt = pCt + 1
p$(pCt) = pe$
END IF
END IF
NEXT
PRINT
FOR i = 1 TO tCt: PRINT t$(i); " "; : NEXT: PRINT
FOR i = 1 TO sCt: PRINT s$(i); " "; : NEXT: PRINT
FOR i = 1 TO pCt: PRINT p$(i); " "; : NEXT: PRINT
PRINT
FOR i = 1 TO tCt
FOR j = 1 TO sCt
FOR k = 1 TO pCt
o$ = t$(i) + s$(j) + p$(k)
good = 1
FOR l = 1 TO LEN(o$) - 1
IF INSTR(l + 1, o$, MID$(o$, l, 1)) THEN good = 0: EXIT FOR
NEXT
miss = 0
IF good THEN
FOR l = 1 TO 9
IF INSTR(o$, LTRIM$(STR$(l))) = 0 THEN miss = l
NEXT
IF miss > 0 THEN
PRINT miss; t$(i); " "; s$(j); " "; p$(k)
END IF
END IF
NEXT
NEXT
NEXT
The program also lists what the valid triangular, square and pentagonal numbers in the given ranges are:
10 15 21 28 36 45 78 91
169 196 256 289 324 361 529 576 625 729 784 841 961
1247 1426 1520 1820 1926 2035 2147 2380 2501 3015 3290 3725 3876 4187 4510 5017 5192 5370 6305 6501 6902 7315 7526 9087 9560 9801
|
|
Posted by Charlie
on 2008-12-16 17:53:55 |



