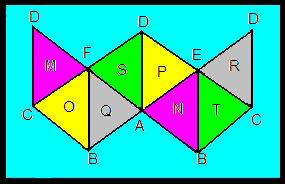
M, N, O, P, Q, R, S and T are the values of the respective sums of the three vertices which form the respective surfaces to which each is assigned.
M + N = O + P = Q + R = S + T
Find unique sets of values1 for A, B, C, D, E and F such that the values of M through T (but not necessarily in that order) form series which increment by 2 of which there are 7.
Background statistics:
Unique Actual
M+N= Interval Sets2 Solutions
21 1 1 96
23 1 2 96
25 1 2 96
26 2 2 96
27 1 5 480
29 1 4 288
30 2 3 144
31 1 8 288
33 1 6 480
34 2 2 96
35 1 2 96
37 1 2 96
39 1 1 96
40 2448
Note:
1. For M+N=21,
1, 2, 3, 6, 4, 5
1, 2, 3, 6, 5, 4
and 1, 2, 5, 3, 4, 6
are the first 3 of 96 solutions. The 96 values do not
discriminate amongst vertex rotation or reflections.
2. Each unique set configures the octahedron in more ways than one.



