The network represents a map of the edges and vertices of a
hypercube or more precisely, a tesseract when imposed within 2D space.
 |
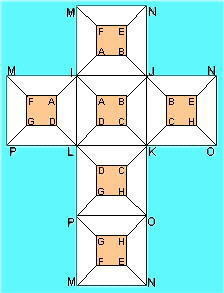The orange squares represent the faces of the internal cell, a cube in 3D space, and is defined by vertices A to H. The larger bolder letters, I to P are the vertices of the outer cell/cube.
The diagonal lines are the edges which link the inner to the outer forming the faces that configure the cells which interface to the inner and outer cells.
Let each hypercell have a value which is the vertex sum of each of its enclosing faces (or three times the sum of its 8 vertices).
|
The vertices are to be numbered uniquely from 1 to 16, and for consistency of reference, let
A always be 1.
Find sets of values for A through P so that all the cells have the same value.
Note: while the on-line calculator may be useful, a spreadsheet should prove more valuable for those able to use one.
(In reply to
re: computer solution by Charlie)
Quoting Charlie:
However, I noticed that while cell ADFGILMP is used in the calculator portion, and, based on that, in my computations, that the diagram shows cell ACFGILMP. There had been mention in the queue of a mix-up between C and D, and I think that mix-up is still present.
Charlie was quite correct that the graphic did not match the body text, a correction re the placement of C & D was erronously made and appeared in the public arena.
Levik has since installed what I now hope is the correct image. (Thanks Charlie, thanks levik).
Edited on February 3, 2009, 11:10 pm
|
|
Posted by brianjn
on 2009-02-03 20:09:41 |
re(2): computer solution [graphic error]
