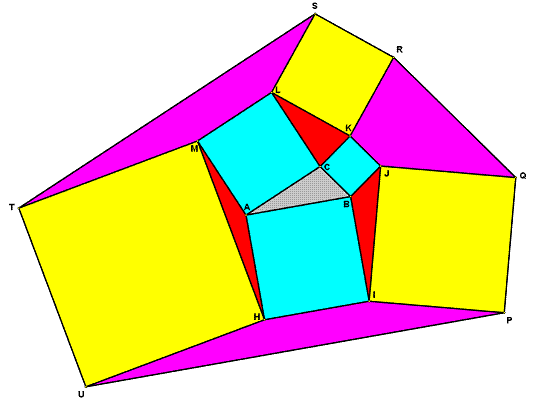
For the arbitrary triangle ABC in the figure below, prove that:
1) The yellow area is three times the cyan area.
2) The magenta area is five times the red area.
Note: The yellow and cyan areas are squares.
(In reply to
yellow/cyan proof by Daniel)
Building on your proof. Finding the Magenta areas requires finding the area of a quadrilateral when 3 sides and the two enclosed angles are known (SASAS). I attempted to derive a formula for this.
Let the sides be a, b, and c with angle X between a and b and angle Y between b and c.
Area = .5(ab(sin(X))-bc(sin(Y))+ac(sin(Y-X))
this formula does not seem to work though so we cant use it to continue.
|
|
Posted by Jer
on 2009-06-17 14:23:39 |



