Place the numbers 1-9 in the boxes so that the difference of each pair of numbers joined by a line is at least three. The number 8 has already been placed.
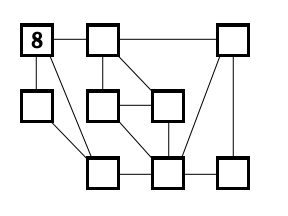
The puzzle is solvable even when the 8 is replaced by 1, 2, 4 or 6. The solution to the current puzzle (i.e., with 8 at upper left) is the last pair below. Solutions come in pairs as the second and third numbers in the middle row can always be interchanged.
1 8 3
7 2 5
4 9 6
1 8 3
7 5 2
4 9 6
2 7 3
8 1 4
5 9 6
2 7 3
8 4 1
5 9 6
4 8 3
7 2 5
1 9 6
4 8 3
7 5 2
1 9 6
6 2 7
3 5 8
9 1 4
6 2 7
3 8 5
9 1 4
8 3 7
2 6 9
5 1 4
8 3 7
2 9 6
5 1 4
DECLARE SUB addOn (p!)
DATA 247,1563,289
DATA 17,268,258
DATA 418,75639,83
CLS
DIM SHARED con$(9), numval(9)
FOR i = 1 TO 9
READ con$(i): PRINT con$(i); "."
NEXT
DIM SHARED used(9)
FOR n = 1 TO 8
used(n) = 1
numval(1) = n
addOn 2
used(n) = 0
NEXT
SUB addOn (p)
FOR n = 1 TO 9
IF used(n) = 0 THEN
good = 1
FOR j = 1 TO LEN(con$(p))
psn = VAL(MID$(con$(p), j, 1))
IF psn < p THEN
IF ABS(numval(psn) - n) < 3 THEN good = 0: EXIT FOR
END IF
NEXT
IF good THEN
numval(p) = n
used(n) = 1
IF p < 9 THEN
addOn p + 1
ELSE
PRINT numval(1); numval(2); numval(3)
PRINT numval(4); numval(5); numval(6)
PRINT numval(7); numval(8); numval(9)
PRINT
END IF
used(n) = 0
END IF
END IF
NEXT
END SUB
|
|
Posted by Charlie
on 2010-08-04 13:56:24 |





