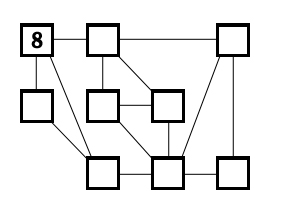
Place the numbers 1-9 in the boxes so that the difference of each pair of numbers joined by a line is at least three. The number 8 has already been placed.
(In reply to
re: solution by reasoning by ed bottemiller)
Ed,
It took me very short time to solve the puzzle while it was on the review board. The reasons I did not rush to post it as soon
as I saw it published were :
a)I do not like to provide just answers with no explanation .
b) In this case, as in many others, solving was much easier and faster than summing up the process of finding a qualifying answer.
In a nutshell,- while reading the post I grasped the division of 9 digits into a rich set R(1,2,8,9) and poor set P(3,4,5,6,7).
Member of R have 5 eligible numbers as neighbors,the rest only 4.
Calling the squares asv follows: ABC -upper row; DEF -mid and GHI low and counting the branches outgoing from each of them - I get H as calling for a member of the R set, i.e. 1,2, or 9 -8 being placed in A by problem's initial condition.
Assigning 1 to H, D could be either 4 or 5.
etc etc
I continue in this way, keeping track of used (spent) links.
This process cannot be called analytical, but is not an "exaustive "
search (checking each of 8! possible permutations) but rather a selective and ordered sequence of trying at each stage to advance with the most likely candidate.
Once reaching a solution - no need, other than curiosity, to prove uniqueness or look after additional solution.
I believe that you did not use a blind comprehensive search and since you have forced me to spend 33 minutes to write doen what took 6-7 minutes to solve - i would like you to reciprocate with a short description of your method.
As they say: I've shown you mine , now show me yours.
t





