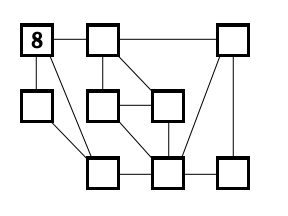
Place the numbers 1-9 in the boxes so that the difference of each pair of numbers joined by a line is at least three. The number 8 has already been placed.
(In reply to
re: solution by reasoning by ed bottemiller)
It is 03:25 AM and this is probably the best excuse for so many errors in my explanation . <o:p></o:p>
It was G=5, not C and now I write while viewing both the diagram and my solution. <o:p></o:p>
<o:p></o:p>
<o:p></o:p>
837 UPPER ROW ABC<o:p></o:p>
296 MID DEF <o:p></o:p>
514 BOTTOM ROW GHI<o:p></o:p>
<o:p></o:p>
Start H=1 <o:p></o:p>
G is between 1 and 8,
so 4 or 5 are candidates, <o:p></o:p>
Choosing G=4 leaves no choice for D , <o:p></o:p>
so G=5 and D=4<o:p></o:p>
We now have <o:p></o:p>
<o:p></o:p>
8 B C<o:p></o:p>
5 E F<o:p></o:p>
2 1 I<o:p></o:p>
<o:p> </o:p>
There are only two digits left with only 2 possible neighbors: 4(neighboring 6 or 9) and 6(3 or 9) .<o:p></o:p>
One of those has to be placed in I, the only box with 2 links only. <o:p></o:p>
Placing 6 leads to a dead end forcing C=9 thus leaving no choice for B . so the choice is I=4 ,C=7 and B =3.
6 and 9 go to E and F or F and E.
Hopr there are no errors .
<o:p></o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p></o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
es no choice for c therefore i=4 and c f<o:p></o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>
<o:p> </o:p>





