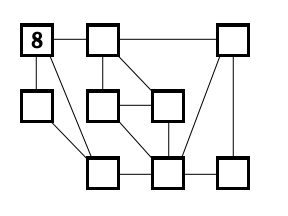
Place the numbers 1-9 in the boxes so that the difference of each pair of numbers joined by a line is at least three. The number 8 has already been placed.
I appreciate your descriptions of approaches to this puzzle. I do think that puzzles should have unique and exhaustive solutions (though I would not disqualify this puzzle by the interchange of values for the two center boxes).
We probably all have varying reasons for trying to solve puzzles of this sort -- all perfectly legitimate. Some value mostly highly being able to solve by chains of deduction, without recourse to computers or other aids. For myself (because of vocation), I place high value on being able to find a computer program to express a method of solution, and within that to appreciate methods which are more efficient (and still accurate). The latter may indeed overlap with the 'analytic only' approach, in the finding of more efficient code. One consideration would be the relative amounts of time to reach a solution by these different approaches. I also appreciate the responses of those, such as Charlie, who gives computer code (or sometimes, the pseudo-code outline) for their approaches -- I learn from these, even when I have a different environment. This also applies to those who suggest extensions or variations on a given problem (especially when the original has been solved), e.g. finding which variants on the upper left box (8, or other) have solutions -- may pursue these depending upon available time and interest.
There are some cases where problems may be intractable without assistance. For example, if a program dealing in rather large numbers has "being prime" as a condition, I would think it legitimate to use tables or a computer language with an "is prime" function, rather than trying to factor all candidates. The recent "Garden of Pythagoras" puzzle by Broll would be a similar case, where solution by hand would be onerous (though the text suggests that Pythagoras did it "in his head").
In the current instance, I assigned letters to the nine squares, regarded each as a distinct variable 1..9 without reuse, and loop tested each configuration for the required "different from attached squares by three or more" rule. This took perhaps 20 to 30 minutes to code and debug, but found the solutions in under a second of "wall time". Also, when the variation was suggested, it literally took only a few seconds to recode one line for a different seed value in the upper left corner (as discussed with Charlie in earlier posts). My rule of thumb is to look for the quickest solution overall (analysis + coding/testing, if needed). I did spend a few minutes at the start to see if an "analytic" solution appeared, but did not find one, so wrote a short program. I could have made the program faster by eliminating some lines through Ady's method of limiting possible values for various squares by counting connectors, but it would have taken longer to code that. By my own criterion, Ady solving this in seven minutes would beat my time -- perhaps I quit too soon on the guided trial-and-error approach.
Some of the Perplexus puzzles can indeed be solved with a few minutes reflection, whereas others probably require some calculation assistance. I do, however, have less patience with those which are not unambiguously stated -- a first lesson in computing is to know exactly what you are trying to solve before starting. The more the merrier -- chacun à son gout!





