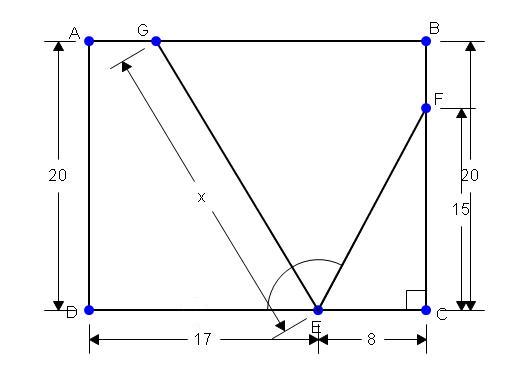
|ED| = 17 = |EF|  and

angle DEG = angle FEG. Therefore,

Triangles DEG and FEG are congruent.

Thus, |DG| = |FG|. Therefore,

  20^2 + |AG|^2 = |DA|^2 + |AG|^2

                = |DG|^2 = |FG|^2

                = |GB|^2 + |BF|^2

                = |GB|^2 + 5^2

                or

  |GB|^2 - |AG|^2 = 20^2 - 5^2

                or

  (|GB| - |AG|)(|GB| + |AG|)

  = (|GB| - |AG|)(25) =  (20 - 5)(25)

Thus,

  |GB| - |AG| = 15

  |GB| + |AG| = 25

Therefore, |AG| = 5. Thus,

  |EG| = sqrt(|DA|^2 + [|DE| - |AG|]^2)

       = sqrt(20^2 + 12^2) 

       = sqrt(544) ~= 23.3238