Two rectangles, shown below, are drawn on an isometric grid whose closest points are 1m apart. Draw a square whose vertices coincide with grid points, or prove that no such square exists.

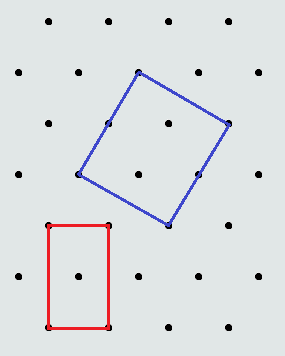
The sides can't be vertical and horizontal, as the horizondal ones would have an integral side length while the vertical would be irrational.

Start out with the leftmost corner of the potential square. One of the adjacent vertices will be down and to the right of the first, and the other will be up and to the right.

Let the one that is down and to the right be a/2 meters to the right of the first and b rows of dots down (b*sqrt(3)/2 meters down), where a and b are either both even or both odd.

Let the one that is up and to the left be c/2 meters to the right of the first and d rows of dots up (d*sqrt(3)/2 meters up), where c and d are either both even or both odd.

The two adjacent sides must be at right angles to each other so their slopes must have a product of -1. The first side has slope -b*sqrt(3)/a and the second has the slope d*sart(3)/c, so

3*b*d/(a*c) = 1

so c/d = 3*b/a

But the sides must also be equal in length, so

c^2 + 3*d^2 = a^2 + 3*b^2

The following program looks for a, b, c and d that fit.

The variable cod is c/d (c over d).

DEFDBL A-Z
CLS
FOR a = 1 TO 20
  offset = a MOD 2
  FOR b = offset TO 200 STEP 2
    cod = 3 * b / a
    FOR d = 1 TO 200
      c = d * cod
      crnd = INT(c + .5)
      IF ABS(crnd - c) < .00000001# THEN
        c = crnd
        IF c MOD 2 = d MOD 2 THEN
          IF c * c + 3 * d * d = a * a + 3 * b * b THEN
               PRINT a; b, c; d, (a * a + 3 * b * b) / 4
          END IF
        END IF
      END IF
    NEXT d
  NEXT
NEXT

The division of the "area" by 4 reflects the fact that we're dealing with half-meters in determining the square of one side and we want to measure square meters.

However, the program finds no solutions.

This does not mean that if we increased the covered area even more that we wouldn't find a square, but I doubt that the rational/irrational situation can be overcome.

Posted by Charlie on 2012-09-16 20:53:47