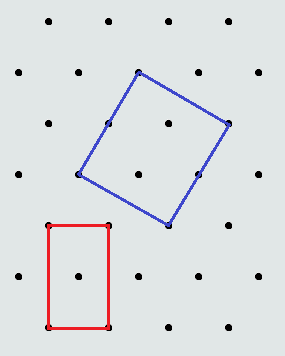
Two rectangles, shown below, are drawn on an isometric grid whose closest points are 1m apart. Draw a square whose vertices coincide with grid points, or prove that no such square exists.

(1) Count dots along the x-axis from the origin, 1,2,3,4...until, say, the 2849533762217005969423814659495539159748916737th dot is reached. Call this, a.
(2) Similarly, count dots along the y-axis from the origin, 1,2,3,4... until, say, the 1645179084680915450976475899442387834431551584th dot is reached. Call this, b.
(3) join up the dots to form a square: (0,0),(a,0),(0,b),(a,b).

You will need a big piece of paper. Assuming one used a piece the size of the known universe, it seems the distances between dots would still be unmeasureable by any instrument.

 

 

 

Edited on September 17, 2012, 1:18 am

Posted by broll on 2012-09-17 01:12:46