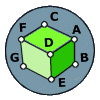
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).

A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).

If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?

The path does not have only to go through the midpoint of FD or DE. Any edge that does not include A or G is equivalent because they are opposite corners (the fact that you can't see them in the given diagram changes nothing). So, the shortest paths connect straight lines through CF, FD, DE, EB, and BX and CX (where X is the point on the 'far' side of the cube, and not shown in the picture). Each of these points is √3/2 from both A and G.

Posted by DJ on 2003-05-22 17:01:27