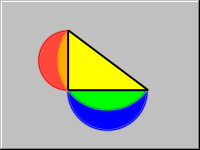
Given a right triangle, draw the three following semicircles:
- The semicircle with diameter formed by one of the legs and extending away from the triangle.
- The semicircle with diameter formed by the other leg and extending away from the triangle.
- The semicircle with diameter formed by the hypotenuse and extending towards the triangle.
Prove that the area of the two crescents (shown in RED and BLUE) formed by the three semicircles equals the area of the triangle.
I didn't really follow the folding proof, so here's my own.
Construct line AH dividing the big triangle into 2 smaller ones with right angles at H.
Call the area of triangle ABC, a.
Call the area of triangle AHC, b.
Call the area of triangle ABH, c.
Clearly, b+c=a
Call the circle whose diameter is BC, C1
Call the circle whose diameter is AB, C2
Call the circle whose diameter is AC, C3.
Since b+c=a, and since the the diameters of the circles are the same as the sides of triangle ABC, so the areas of the circles are in the same proportion as the areas of the triangles.
C2+C3=C1
Now, (1/2C1-a) is the area outside a, but enclosed by C1, and
(1/2C2+1/2C3) is the area of the two smaller circles outside a, so
the area of the lunes is (1/2C2+1/2C3)-(1/2C1-a).
But (1/2C2+1/2C3)=(1/2C1), so (1/2C2+1/2C3)-(1/2C1)=0.
The area of the lunes =-(-a) = a, so the lunes have the same area as triangle a.
Edited on February 3, 2016, 11:03 am
|
|
Posted by broll
on 2016-02-03 05:17:04 |
 Given a right triangle, draw the three following semicircles:
Given a right triangle, draw the three following semicircles:


