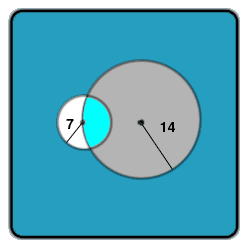
A circle has a radius of 14 cm. Another circle has a radius of 7 cm. The centre of the second circle lies on the circumference of the first. Find The common area for both circles.

(P.S -The answer might not be elegant)

There is a formula here for the lune, i.e. the part of the size 7 circle that is not common. For generalisation, call 7 a for a moment.

This does allow a lot of cancellation:

Starting with the easy part, delta:1/4*((a+2a+2a)(2a+2a-a)(2a+a-2a)(a+2a-2a))^(1/2), simplifying to:

(15^(1/2)a^2)/4. Two of these are required: (15^(1/2)a^2)/2

Then the harder part:a^2[ArcSec((2*a*2a)/((2a)^2-a^2-(2a)^2)))]-(2a)^2[ArcSec((2*2a*2a)/((2a)^2+(2a)^2-a^2)))]. Again much simplification is possible:

a^2[ArcSec(-4)]-4a^2[ArcSec(8/7)], or a^2([ArcSec(-4)]-4[ArcSec(8/7)])

So the generalised solution is:  pi*a^2-(a^2([ArcSec(-4)]-4[ArcSec(8/7)]) +(15^(1/2)a^2)/2) or simply:

1.40307a^2. Solving for a=7, this gives 68.75043.

For a much higher degree of accuracy,  compute [ArcSec(-4)]-4[ArcSec(8/7)] first, namely -0.19796545919965395516828036731622536366677143199031444494

giving

1.40306643968573875104129105070452844244747997871962485262a^2, or in this example:

68.7502555446011988010232614845218936799265189572616177774, probably close enough for most purposes.

Edited on June 10, 2016, 5:47 am

Posted by broll on 2016-06-10 05:21:02