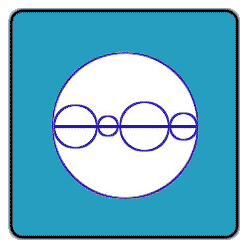
Prove that the sum of the perimeters of the smaller circles in the Bigger circle is equal to that of the bigger circle. (The centres are on the line given which is the diameter of the bigger circle.)

this one was no problem
calling the first small circle circle 1 with a diameter of AB, the 2nd small circle circle 2 with a diameter of BC, the 3rd small circle circle 3 with a diameter CD, the 4th small circle circle 4 with diameter DE and the large circle circle 5 with a diameter AE
we want to prove that- circumfrence1+circumfrence2+circumfrence3+ circumfrence4= circumfrence5

1) AB+BC+CD+DE=AE - because the whole ='s the sum of its parts

2) Circumfrence1=piAB
Circumfrence2=piBC
Circumfrence3=piCD Circumfrence4=piDE
Circumfrence5=piAE
because the equation for the circumfrence of a circle is C=pi(d)

3) pi(AB+BC+CD+DE)=piAE you can multiply both sides of the equation in step1 by any varible without changing the value of the equation

4)piAB+piBC=piCD+piDE=piAE this is simple multiplying

5)circumfrence1+circumfrence2+circumfrence3+ circumfrence4= circumference5
this is just simple substitution

Posted by joy on 2003-06-16 18:24:31