perplexus.info :: Numbers : Olympic Rings

Olympic Rings (Posted on 2008-06-04)

When overlapped the 5 Olympic rings enclose 9 regions.

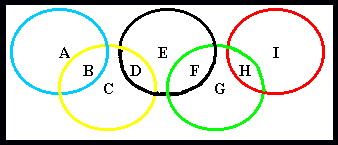
Place each of the numbers from 1 to 9 in a separate region so that:

A + B = B + C + D = D + E + F = F + G + H = H + I = M

where M represents the total of each ring.

How many values for M can you find?
How many arrangements for each M can you also find (discount total reversal of order)?

See The Solution Submitted by brianjn

Rating: 4.0000 (1 votes)

Comments: ( Back to comment list | You must be logged in to post comments.)

Puzzle Thoughts

| Comment 7 of 8 |

M=11

(A,B,C,D,E,F,G,H,I)=(9, 2, 5, 4, 6, 1, 7, 3, 8)

M=13

(A,B,C,D,E,F,G,H,I)=(9, 4, 1, 8, 3, 2, 5, 6, 7)

(A,B,C,D,E,F,G,H,I)=(7, 6, 5, 2, 8, 3, 1, 9, 4

M=14

(A,B,C,D,E,F,G,H,I)=(8, 6, 1, 7, 4, 3, 2, 9, 5)

Posted by K Sengupta on 2023-01-21 23:54:51

Please log in:

Login:
Password:
Remember me:

Sign up! \| Forgot password

Search:

Search body:

Forums (0)
Newest Problems
Random Problem
FAQ | About This Site
Site Statistics
New Comments (3)
Unsolved Problems
Top Rated Problems
This month's top
Most Commented On

Chatterbox:


perplexus dot info