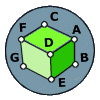
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).

A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).

If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?

To solve this, it is easiest to think of part of the cube on a plane. Take faces FDAC and GEDF. Think of them as flattened on a plane. Since the shortest distance between any two points is a straight line, draw the line from A to G. Now, put them back on the cube. The line the fly should follow should go from A to a point that bisects segment FD, and then to G.

Posted by ethan on 2003-08-10 12:54:36