Prove or disprove, that the points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle. (In other words, that for any yellow triangle, the green triangle will be equilateral, given that the thinner lines trisect their respective angles.)

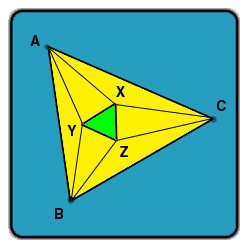
Imagine a triangle composed by sides A, B, C and angles thetaA, thetaB, thetaC (the opposite side of thetaA is A, the opposite side of thetaB is B and the opposite side of thetaC is C). Align such triangle to a Cartesian coordinate plane (X axis and Y axis) in a way that the vertex in thetaA touches the origin of the X axis and Y axis, also the vertex at thetaC touches the X axis pointing towards +infinite. To calculate the sides of the special triangle, I used intersecting linear equations, and the coordinates of such special triangle are:
X1=C*sin(thetaB/3)*tan(thetaA+thetaB/3)/(sin(thetaA+thetaB/3)*[tan(thetaA+thetaB/3)-tan(2*thetaA/3)])
X2=B*tan(180-thetaC/3)/(tan(180-thetaC/3)-tan(thetaA/3))
X3=B*sin(thetaC+thetaB/3)*[tan(180-thetaC-thetaB/3)-tan(180-2*thetaC/3)]-A*sin(thetaB/3)*tan(180-thetaC-thetaB/3)/(sin(thetaC+thetaB/3)*[tan(180-thetaC-thetaB/3)-tan(180-2*thetaC/3)])
Y1=X1*tan(2*thetaA/3)
Y2=X2*tan(thetaA/3)
Y3=(B-X3)*tan(2*thetaC/3)
The distances of such triangle can finally be tested and prove that it is an equilateral triangle or not.
L1=√((X2-X1)²+(Y2-Y1)²)
L2=√((X3-X2)²+(Y3-Y2)²)
L3=√((X3-X1)²+(Y3-Y1)²)
If such triangle is equilateral then L1, L2 and L3 must all be the same length. An examples:
1.- A triangle with thetaA=30 degrees, B=10 and C=6, has an equilateral special triangle with sides L1=L2=L3= 0.92271409
2.- A triangle with thetaA=50 degrees, B=3 and C=4, has an equilateral special triangle with sides L1=L2=L3= 0.5862669748
Solution: the special triangle is always an equilateral triangle.
Note: With the values of thetaA, B and C you can find all other values for a real existent triangle using the law of cosines.

Posted by Antonio on 2003-09-01 04:22:23