A name which has nothing to do with this question (well almost nothing)

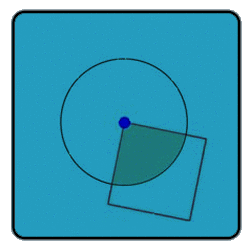
What percentage of the circle is shaded? (The quadrangle shown in the picture is a square with one of the vertices in the circle's center.)

(In reply to Solution by manolo)

By "undefined, I assume you meant "not well defined" and were thinking that there would not be enough information to solve it>

There's a thought. Assuming e, the edge of the square is less than r, the radius of the circle, but greater than r/ (√2), can we determine A, the area of the region common to both shapes?

(We already know that if e ≥ r, the area is πr²/4; and if e ≤ r/(√2) the area is e²)

To me it seems pretty straightforward. The answer will be best expressed as a function [f(e)] of the variable e expressed as a fraction of r.

Hint: Although the greater function becomes discontinuous at e = r and e = r/(√2), the value of the function does not, so A = f(e) should equal πe²/4 when e = r and e² when e = r\(√2).

Posted by TomM on 2002-07-18 07:09:15