Look at this shape:

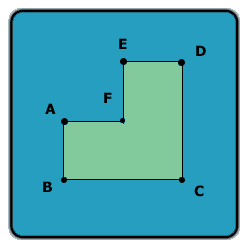
Assume AB = AF = FE = ED and BC = CD, and all the angles in the shape are 90 degrees.

Let A be the area of this shape (in cm^2), and P -- the perimeter of this shape (in cm).

If A - P is 60, what is the length of line AC?

The answer is: the square root of 180 (approximately 13.416).

Steps:

1. The equation for the length of each full side:
((x ^2) * 0.75) - (4x) = 60

The solution to this is 12

2. Therefore, the length of AB is 6 and BC is 12

3. Therefore, according to Pythagorean theorem, ((6 ^ 2) + (12 ^ 2)) ^ 0.5 = square root of 180, or 13.416 (approx.)

Posted by J Miesch on 2003-10-17 11:48:53