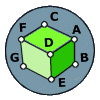
Consider the cube shown (assume for argument's sake that it's a perfect cube, contraty to what the picture may look like).
A fly, sitting in the vertex (A) of this cube must travel the surface of the cube until it arrives at the vertex (G).
If the fly cannot leave the surface of the cube, what is the shortest path for the fly to take between the two points?
If we have a point, M, that is the midpoint of FD then we know that the distancee AM is the same as MG. We can calculate the distance AM (and therefore MG) with some simple use of pythagoras' theorem. If we use x as the side length of the cube:
AM = √(x² + (x/2)²)
AM = (√(5)x)/2
Therefore:
AG = 2AM
AG = √(5)x
This can be compared to Karen's proposal of A->F->G, where:
AF = √(2)x
and
FG = x
therefore:
AFG = √(2)x + x
Which is greater than √(5)x for all positive values of x.
I know that this is not a definitive mathematical solution, but I hope this helps.
Cheers,
Dave
Solution (Mathematical)
