2 Colors 2 (Posted on 2003-08-25)

	Submitted by DJ
Rating: 4.3684 (19 votes)
Solution:	(Hide)
Five points are needed. Take any two points that are of different colors; let's say that they are blue and orange. The midpoint of the segment connecting the two points must be one of the two colors; therefore, it will match one of the vertices. Let's assume it is blue. From the blue midpoint and the blue endpoint, there are two points equidistant from both, forming two equilateral triangles. If either of these points is also blue, then they will, of course, form a monochromatic equilateral triangle. However, if both points are orange, they are vertices of another equilateral triangle, formed with the first orange point. 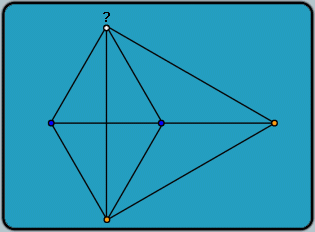Therefore, there must exist an equilateral triangle whose vertices are all the same color, and we have proven this using only five points.

	Subject	Author	Date
	Puzzle Thoughts	K Sengupta	2023-05-12 22:44:54
	selecting points	keiko	2004-06-27 18:41:15
	No Subject	B M	2003-09-29 04:46:38
	re(3): 5-point proof - to DJ	Charlie	2003-09-21 16:34:10
	re(2): 5-point proof - to DJ	aln	2003-09-20 23:12:44
	How about ...	Lawrence	2003-08-30 20:42:11
	re(4): 5-point proof	DJ	2003-08-26 21:14:49
	re(3): 5-point proof	Kelsey	2003-08-26 20:59:23
	re(2): 5-point proof	DJ	2003-08-26 16:51:48
	re(2): 5-point proof	Kelsey	2003-08-26 15:39:07
	re: 5-point proof	Kelsey	2003-08-26 15:29:18
	5-point proof	Bryan	2003-08-26 10:59:20
	Another proof	Brian Wainscott	2003-08-25 17:35:34
	a proof	Charlie	2003-08-25 13:17:23