
Home > Shapes
| Bat wings (Posted on 2005-06-08) |
 |
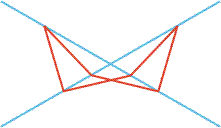
In the picture all of the red segments are of equal length and all of their endpoints lie on one of the two blue lines. Determine all possible values for the smaller angle between the blue lines.
(This problem is a special case of a problem discovered by Daniel Shapiro, professor of mathematics at Ohio State University. His problem generalizes a problem he saw years ago.)
|
|
Submitted by McWorter
|
|
Rating: 4.3333 (3 votes)
|
|
|
Solution:
|
(Hide)
|
|
Hopefully, it will be easier to follow the discussion if we look at the problem backwards. Let A, B, C, etc., be the vertices in clockwise order of a regular polygon or star polygon, and let O be any point on the circle circumscribing the polygon. Then the angles AOB, BOC, etc., are all equal. Fold up this figure accordion style along the lines OA, OB, etc.; that is, fold along OB so that C lands on OA. Next, fold along OC so that D lands on OB. Then fold along OD so that E lands on OA. Continue in this way until all points are folded onto the two lines OA and OB and the last fold puts A back to its original position. It can happen that we must cycle twice through the points of the polygon before A gets back to its original position. The final result could look like the figure for this problem. (So we expect that the polygon from which this figure came is either a regular hexagon or an equilateral triangle.)
To show that the figure came from the above folding process, we need to show that, given two consecutive red lines, the angle between one of them and the reflection of the other is constant. Let O be the intersection of the blue lines. Let A be the lower rightmost point where a red line meets a blue line. Let B be the upper rightmost point where a red line meets a blue line. The red lines form a closed path. Starting from A, follow the red line path from A to B, to C, to D, to E, to F, and back to A. We show that, if we reflect BC about the blue line containing B, the reflection makes an angle of 2theta with AB extended, where theta is the smaller angle between the blue lines. In fact, given any two consecutive lines along the red path, the second line reflected about the blue line through the intersection of the two consecutive red lines always makes an angle of 2theta.
Let BC' be the reflection of BC about OB. Extend AB to AX. We show that angle XBC'=2*angle BOA. Let theta=angle BOA, omega=angle OBC, and tau=angle BAC. Since the red lines are of equal length, triangle ABC is isosceles and so tau=angle BCA. Hence tau=angle BOA+angle OBC=theta+omega (using triangle OBC). Now,
angle XBC'=angle XBO-angle C'BO=angle XBO-omega=
=theta+tau-omega=theta+tau-(tau-theta)=2theta.
The same argument (with only minor modifications) works for any two consecutive red lines. Hence the red lines unfold to an equilateral triangle or a regular hexagon. Since the red lines are not confined to spanning just one angle between the blue lines, retracing of the polygon must occur and the polygon is an equilateral triangle. Hence 2theta=360/3=120 degrees and so theta=60 degrees. |

Comments: (
You must be logged in to post comments.)
|
 |
Please log in:
Forums (0)
Newest Problems
Random Problem
FAQ |
About This Site
Site Statistics
New Comments (4)
Unsolved Problems
Top Rated Problems
This month's top
Most Commented On
Chatterbox:
|



