|
Creating a "concrete" visual of this may seem horrendous. Once that is done there is really little mathematics left.
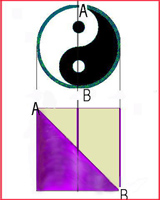
Consider this reckless diagram as the top view of the Yin-yang cylinder being composed of 3 cylinders; the larger has two "sleeves" to carry two cylinders which are exactly half the diameter of the larger.
A
// \\
| \ / |
| / \ |
\\ //
B
By area, each part of the diagram is 1/4 of the larger circle, which does translate to 1/4 of the volume of the cylinder.
A 1 2
|\ | |
| \ | |
| \| |
| |\ |
| | \ |
| | \|B
Now one half of the larger cylinder sliced obliquely from A to B is 1/8 of the whole.
Consider the diagram above to be the two smaller "sleeved" cylinders sliced obliquely from A to B. The lower triangle, under column 2 represents 1/4 of the volume of that cylinder, or 1/16 of the whole.
The 1/8 of the outer plus the 1/16 represent 3/16 of the total volume. The compliment of this is therefore 5/16.The cylinder is therefore divided into four such that
two parts are 18.75% and the others are 31.25%.
If I have gone too fast for some,
consider the small circles to be of radius "1" and the larger "2". Πr2 yields 1*Π and 4*Π. Since the two smaller cylinders are 1/4 of the volume then the two remaining parts of the "main" cylinder are 1/4 each.
It is important to make an acknowledgment. Leming has gone to a lot of work to give the mathematics of this situation. In actual fact I did go through exactly the same process before I realised that there was an 'intuitive' solution, but that does depend a little upon past knowledge.
Read Leming |