Tic-Tac-Toyola is a variation of Tic-Tac-Toe with money. Instead of naughts and crosses (0s and Xs for Americans) being placed at the whim of alternating players, players vie for placement control at each turn by bidding some amount in a currency from an account under their control. The high bid decides the placement, with that bid amount being deducted from the corresponding player's account. Bids are in continuous units, so we can neglect the possibility of tie bids as unlikely.
There are two players: C(rosser) and N(aughty). X is placed first, and player C is declared winner if 3 Xs appear in a row before 3 Os appear in a row. If neither player achieves three in a row, N is declared winner. Thus, a game of Tic-Tac-Toyola will always have a winner.
C and N have been playing for some time and have reached the position:
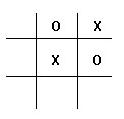
(1) Assuming players are following optimal strategies, show that the outcome is independent of whether bidding is conducted secretly (by sealed bids) or openly (with players offered at each turn the possibility to outbid their opponent).
(2) Show that a player who is following an optimal strategy would not change his bid if he were to learn his opponent's account balance.
(3) Show that N can force a win if and only if he has in excess of twice as much money as C.
Note: Anyone interested in learning more about the Tic-Tac-Toyola family of games is invited to visit http://www.diplom.org/Zine/S2007R/Mayer/tictactoyola.htm