When overlapped the 5 Olympic rings enclose 9 regions.
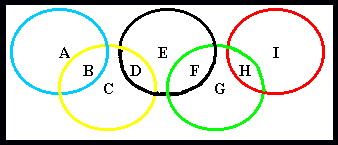
Place each of the numbers from 1 to 9 in a separate region so that:
A + B = B + C + D = D + E + F = F + G + H = H + I = M
where M represents the total of each ring.
How many values for M can you find?
How many arrangements for each M can you also find (discount total reversal of order)?
|
|
Submitted by brianjn
|
|
Rating: 4.0000 (1 votes)
|
|
|
Solution:
|
(Hide)
|
M=11
9, 2, 5, 4, 6, 1, 7, 3, 8
M=13
9, 4, 1, 8, 3, 2, 5, 6, 7
7, 6, 5, 2, 8, 3, 1, 9, 4
M=14
8, 6, 1, 7, 4, 3, 2, 9, 5
You will find this almost at the bottom of this page:
http://users.skynet.be/worldofnumbers/ninedig1.htm
A link cited there is no longer valid:
http://freespace.virgin.net/ashley.england/Moment/olympic.htm).
You may find it also at:
http://ken.duisenberg.com/potw/archive/arch97/970725.html
and Wolfram has a demonstration of this:
http://demonstrations.wolfram.com/PandigitalOlympicCirclesPuzzle/ |




