perplexus.info :: Geometry : Mirrors in a Hex

Mirrors in a Hex (Posted on 2009-05-08)

Six vertical mirrors are arranged to form a regular hexagon with only a small gap (of negligible size) at each vertex. A beam of light is shone through one of these gaps toward the one directly opposite, through which it exits.

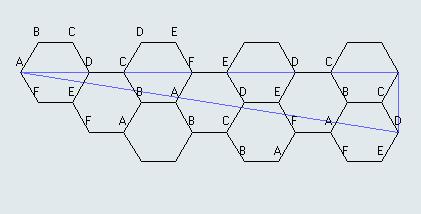
However, the beam can be aimed slightly off this direct route to the other side, so that it is reflected off each of the mirrors exactly once before finally exiting the arrangement through that same opening opposite its entrance.

What is the smallest angle off of straight across which will make this possible?

Submitted by Charlie

Rating: 3.0000 (1 votes)

Solution: (Hide)

arctan(sqrt(3)/11), or about 8.94827556462713 degrees, as seen on the diagram below.
The vertices are labeled in hexagons only according to the reflection through the side actually traversed in the diagram, or reflected from in the actual mirror situation, that is, in the order DE, BC, AF, CD, EF, AB. Some hexagons not traversed have vertices whose labels are from adjoining hexagons.

Based on Enigma No. 1532, "Just Reflecting", by Bob Walker, New Scientist, 14 February 2009, page 26.

Comments: ( You must be logged in to post comments.)

	Subject	Author	Date
	Solution	Bractals	2009-05-08 15:03:37

Please log in:

Login:
Password:
Remember me:

Sign up! \| Forgot password

Search:

Search body:

Forums (0)
Newest Problems
Random Problem
FAQ | About This Site
Site Statistics
New Comments (3)
Unsolved Problems
Top Rated Problems
This month's top
Most Commented On

Chatterbox:


perplexus dot info