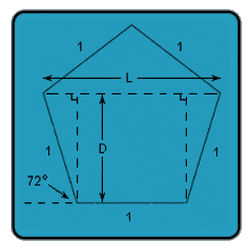
 Each side of the die is a regular pentagon, which have an interior angle of 108° and an exterior angle of 72°. Consider a pentagon with one edge at the bottom and the apex at the top, and set the length of one edge arbitrarily to 1 (regardless of size, all the angles remain the same anyway). If we draw a line parallel to the base, from the left shoulder of the pentagon to the right, then the distance D from the base to the parallel is
Each side of the die is a regular pentagon, which have an interior angle of 108° and an exterior angle of 72°. Consider a pentagon with one edge at the bottom and the apex at the top, and set the length of one edge arbitrarily to 1 (regardless of size, all the angles remain the same anyway). If we draw a line parallel to the base, from the left shoulder of the pentagon to the right, then the distance D from the base to the parallel is
D = 1*sin(72) = 0.95106
and the Length L of the parallel is
L = 1*cos(72) + 1 + 1*cos(72) = 1+2cos(72) = 1.61803
Now consider two adjacent sides of the dodecahedron sharing an edge, for example the pentagon we have been discussing and one sharing its bottom edge, looking like a reflection of the first. Draw a perpendicular on the first pentagon between the base and the parallel. The perpendicular intersects the base at a point we will call B, and it intersects the parallel at point A. Draw a similar perpendicular on the second pentagon, from point B down to the parallel at point C. Angle ABC describes the angle between the two sides.
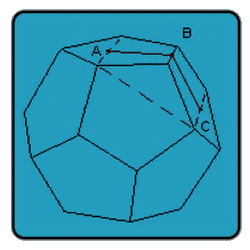
To calculate angle ABC, we simply need the lengths of the three sides. We know that
AB = BC = D = 0.95106
and we need to figure out the length of AC. But because this is a dodecahedron, we know that at either end of the edge shared by the two pentagons is the apex of yet another pentagon that shares an edge with each of the first two. If we draw a line on this last pentagon that connects the ends of the parallels drawn on the first two, we see that it must be true that
AC = L = 1.61803
Now, applying the law of cosines to our problem,
AC^2 = AB^2 + BC^2 –2AB*BC*COS(angle ABC)
solving for ABC
angle ABC = ARCCOS [(AC^2-AB^2-BC^2)/(-2AB*BC)]
angle ABC = ARCCOS[(1.61803^2-2*.95106^2)/(-2*.95106^2)]
angle ABC = 116.564°
|




