|
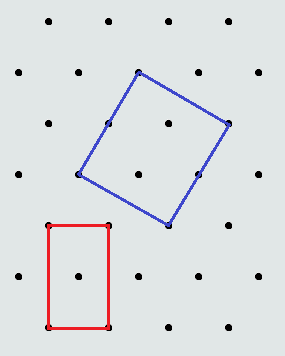
Pick any point on the grid and call it (0,0), and have it be the first point of the square. All other points on the grid are of the form (k/2, m*sqrt(3)), where k and m are integers. In other words, the x-values are all rational, and the y-values are all irrational (except where m=0).
If you choose point (s,t) as the second point of the square, where s and t are both non-zero, the third point must be (t,-s) [or (-t,s)]. But the x-value would then be irrational, and the y-value rational, and therefore does not exist on the grid.
If you choose point (s,0) as the second point, the third point must be (0,s) [or (0,-s)], but then the y-value would be rational, and would not exist on the grid.
If you choose point (0,t) as the second point, the third point must be (t,0) [or (-t,0)], but then the x-value would be irrational, and would not exist on the grid.
Therefore, no third point can exist [other than the trivial (0,0)]. |