Look at this shape:
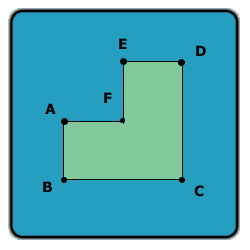
Assume AB = AF = FE = ED and BC = CD, and all the angles in the shape are 90 degrees.
Let A be the area of this shape (in cm^2), and P -- the perimeter of this shape (in cm).
If A - P is 60, what is the length of line AC?
(In reply to
A different angle by Callum)
First, when you came up with a negative value for the length, that should have been a sign that something is wrong.
The problem with your anaysis is, the ratio of A to P is not simply 3/8, it is 3/8 times whatever ab is (or af, de, etc). Then, you would have to "times the area and perimeter" 6, instead of -12, to get the equation 104-48=60, which is equal on each side (in essence, you were trying to solve 3x-8x=60 instead of 3x²-8x=60, which is why you got a negative answer). Once you have the right value for x, the Pythagorean theorem gives AC²=6²+12²=180, so AC is about 13.416.
|
|
Posted by DJ
on 2003-10-10 09:31:00 |



