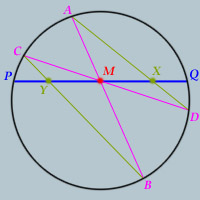
Given a circle and two points on that circle,
P and
Q, draw the chord
PQ, and label its midpoint
M.
Now draw two other chords of the circle AB and CD that both pass through M.
Further, draw chords AD and BC.
Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________
Prove that M is the midpoint of line segment XY.
well... there is a sure-fire way to get MX = MY, which is CPCTC (correspoding parts of congruent triangles are congruent) after either figuring out if triangle CMY is congruent to DMX, or figure out YMB is congruent to XMA... hmm i already notice vertical angles, so mebe u gotta use SAS or SAA?
also... u no that angle D is congruent to angle B because they share the same arc CA. Similarly, angle C and A are congruent because they share the same arc BD.
one more thing... u can prove that triangle CMB is similar to AMD by AAA, but their congruence cant be proven just yet (if possible)
Edited on March 24, 2004, 4:42 pm
No Subject
