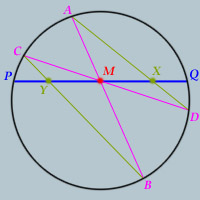
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.

Now draw two other chords of the circle AB and CD that both pass through M.

Further, draw chords AD and BC.

Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________

Prove that M is the midpoint of line segment XY.

(In reply to Answer by Zero Armada)

To say triangles AMD and CMB are symmetrical would be to say they are congruent, but they are not.  Even if they were, MY is on a different side of CMB than the corresponding side of AMD.  In fact, due to the difference in size of the two triangles, this difference allows the compensation to take place in the opposite direction (larger piece of a smaller triangle)-- assuming the theorem is true, which I don't think anyone has proved yet.

Posted by Charlie on 2004-03-25 08:25:39