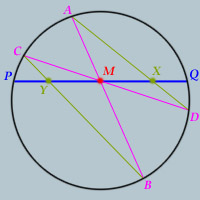
Given a circle and two points on that circle,
P and
Q, draw the chord
PQ, and label its midpoint
M.
Now draw two other chords of the circle AB and CD that both pass through M.
Further, draw chords AD and BC.
Label the intersection of AD and PQ, point X.
Label the intersection of BC and PQ, point Y.
_____________________________
Prove that M is the midpoint of line segment XY.
I came across a reference in one of my books about "The Chord Theorem" which states that:
(using segment lengths) AM:PM = QM:BM.
A similar expression can be derived for chord CD, but none of that seemed to help me.
I propose a solution which looks at the 'limits' of chord CD when it 'would' coincide with chord PQ and chord AB.
In the first instance both C & Y would coincide with P and D & X would coincide with Q thereby rendering M the midpoint of XY. At the other extreme, when C & Y coincide with A, and D & X coincide with B, X, Y and M become the same point.
May I by intuition, using these two extremes conclude that that wherever chord CD is placed (within the parameters of the problem) that M is therefore the midpoint of segment XY?
Edited on July 10, 2004, 8:49 pm
|
|
Posted by brianjn
on 2004-07-10 20:47:28 |
 Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.
Given a circle and two points on that circle, P and Q, draw the chord PQ, and label its midpoint M.


