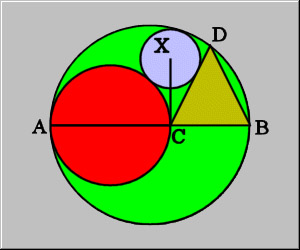
Consider a circle O with a diameter AB, shown here in green. Draw a second circle (red) with diameter AC, such that C is on AB. Draw an isosceles triangle with base CB and third vertex D on circle O. Draw a third circle (X), tangent to the first three figures. Prove that the line from C to the center of circle X is perpendicular to AB.

Let's try this with traditional geometric theory. Given that circle X is tangent to the first three figures, then letting X be the center of that circle.  All radii from X to the points of tangency intersect at 90 degree angles. (If you know your theorems.)

Let E be the tangent point on CD of circle X and F be the tangent point on the circle with diameter AC. Let G be the midpoint of AC and the center of that circle. Now FX = XE since both are radii of circle X.  Because they share a hypotenuse, then triangles CFX and CEX are congruent by hypotenuse-leg theorem.

Extend FX down to G to create triangle GXC.  Extend EX down to B to create triangle BXC, both of which are right triangles.

FC and EC are both altitudes of triangles GXC and BXC, respectively. By geometric means, BX/XC = XC/CE and GX/XC = XC/CF.  Since CE=CF, then BX = GX. Since FX = EX, then GF = EB and we again have congruent triangles GFC and BEC, both of which are right triangles at the tangents with circle X. That makes XT a bisector of GB and because it bisects angle XFE, then it's a perpendicular bisector.  Therefore the angles formed by XC with GB are 90 degrees.

Posted by Celie on 2004-09-11 14:59:47